Research
The research is under the S-STEM program and deals with trying to understand the symmetry in the 12-note western tonal system in its different frequency and octaves. It follows a paper done by professors in the Department of Mathematical Sciences at Appalachain State.
When we say that two notes have a frequency in a 2:1 ratio, they are one octave apart. We give the same name to both notes despite having different frequencies. We will be using modular arithmatic to represent the notes, one can think of a clock about this. in musical terms its \[C, D", D, E", E, F, F#, G, A", A, B", B, C\]
\[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0\]
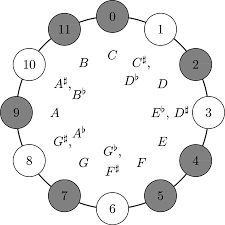
We organize pitch by octaves where frequencies are powers of 2. Two octaves above middle C means that \(2^2 = 4\) times the frequency of middle C. It's intuitively base 2 of a logarithmic scale. We can then transform our "clock" using modular arithmetic to get the circle of fifths which gives the diatonic scales. When in a given key a composer selects notes from a seven-note diatonic scale, so for example the C-major diatonic scale: \[{C, D, E, F, G, A, B} = {0, 2, 4, 5, 7, 9, 11}\]
or the F-major diatonic scale where our \(k = 5\): \[{5, 7, 9, 10, 0, 2, 4}\]
There is also the F to F sharp property When transposing a major scale up by a perfect fifth we obtain a scale with all but one element the same and with the note gained only one semitone above the note lost.
We then started to make our definitions where, a generalized n-note microtonal system with generalized perfect fifth p5 is a division of the octave into n microtones such that each note has a frequency \(2^\frac{1}{n}\) times the previous one. It has the generalized cricle of fifths p5 where its \(\mathbb{Z}_n\). Overall we want it to contain generalized diatonic scales appearing as connected to regions in the generalized circle of fifths with F to F sharp property.
The generalized formulas for microtones:
\(n = 4k\) microtones per octave.
\(p5 = 2k + 1\) as our generalized perfect fifth.
Generalize major diatonic scales are connected regions of \(2k + 1\) notes in the Cayley graph of \(\mathbb{Z}_n = <p5>\)
Now we want to look at our major and minor traids. So the major triad would have a root, note M3 above root, note p5 above root: \[{0, 4, 7} = {C, E, G}\]
While the minor triad has a root, note m3 above root, note p5 above root \[{0, 3, 7} ={C, E", G}\]
the generalized \(M3\) and smaller generalized minor third \(m3\) partition the generalized perfect fifth \(p5\) (i.e. \(M3 + m3 = p5\)) with \(M3\) appearing as an element of the C-major diatonic scale. An additional requirement that ensures that \(M3 = k + 1\) is in the C-major diatonic scale for the \(n = 4k\) note micro- tonal system with \(p5 = 2k + 1\) is that \(M3 = k + 1\) is in the C-major diatonic scale only when k is odd. Therefore n-note microtonal systems meeting our definition must have n a multiple of 4 but not a multiple of 8.